Планиметрия, часть с

Физика 7: все формулы и определения

«Физика 7: все формулы и определения» — это Справочник по физике в 7 классе, доступный для скачивания в 2-х форматах: КРУПНО (формат PDF, на 3-х страницах) и МЕЛКО (формат JPG, на 1-й странице).

1 файл(ы) 255.55 KB

Физика 7 класс: все формулы и определения МЕЛКО на одной странице

1 файл(ы) 549.72 KB

В пособии «Физика 7: все формулы и определения» представлено 24 формулы
и определения за весь курс Физики 7 класса:

Название формулы (закона, правила)	Формулировка закона (правила)	Формула
1. Цена деления шкалы прибора	Для определения цены деления (ЦД) шкалы прибора необходимо: 1) из значения верхней границы (ВГ) шкалы вычесть значение нижней границы (НГ) шкалы и результат разделить на количество делений (N); 2) найти разницу между значениями двух соседних числовых меток (А и Б) шкалы и разделить на количество делений между ними (n).	ЦД = (ВГ — НГ) / N ЦД = (Б — А) / n
2. Скорость	Скорость (ʋ) — физическая величина, численно равна пути (S), пройденного телом за единицу времени (t).	ʋ = S / t
3. Путь	Путь (S) — длина траектории, по которой двигалось тело, численно равен произведению скорости (ʋ) тела на время (t) движения.	S = ʋ*t
4. Время движения	Время движения (t) равно отношению пути (S), пройденного телом, к скорости (ʋ) движения.	t = S / ʋ
5. Средняя скорость	Средняя скорость (ʋср) равна отношению суммы участков пути (S1, S2, S3, …), пройденного телом, к промежутку времени (t1 + t2+ t3+ …), за который этот путь пройден.	ʋср = (S1 + S2 + S3 + …) / (t1 + t2 + t3 + …)
6. Сила тяжести	Сила тяжести — сила (FТ), с которой Земля притягивает к себе тело, равная произведению массы (т) тела на коэффициент пропорциональности (g) — постоянную величину для Земли. (g = 9,8 H/кг)	FТ = m*g
7. Вес	Вес (Р) — сила, с которой тело действует на горизонтальную опору или вертикальный подвес, равная произведению массы (т) тела на коэффициент (g).	Р = m*g
8. Масса	Масса (т) — мера инертности тела, определяемая при его взвешивании как отношение силы тяжести (Р) к коэффициенту (g).	т = Р / g
9. Плотность	Плотность (ρ) — масса единицы объёма вещества, численно равная отношению массы (т) вещества к его объёму (V).	ρ = m / V
10. Момент силы	Момент силы (М) равен произведению силы (F) на сё плечо (l)	М = F*l
11. Условие равновесия рычага	Рычаг находится в равновесии, если плечи (l1, l2) действующих на него двух сил (F1, F2) обратно пропорциональны значениям сил.	a) F1 / F2 = l1 / l2 б) F1*l1 = F2*l2
12. Давление	Давление (р) — величина, численно равная отношению силы (F), действующей перпендикулярно поверхности, к площади (S) этой поверхности	p = F / S
13. Сила давления	Сила давления (F) — сила, действующая перпендикулярно поверхности тела, равная произведению давления (р) на площадь этой поверхности (S)	F = р*S
14. Давление однородной жидкости	Давление жидкости (р) на дно сосуда зависит только от её плотности (ρ) и высоты столба жидкости (h).	p = g ρ h
15.Закон Архимеда	На тело, погруженное в жидкость (или газ), действует выталкивающая сила — архимедова сила (FВ). равная весу жидкости (или газа), в объёме (VТ) этого тела.	FВ = ρ*g*Vт
16. Условие плавания тел	Если архимедова сила (FВ) больше силы тяжести (FТ) тела, то тело всплывает.	FВ> FТ
17. Закон гидравлической машины	Силы (F1, F2), действующие на уравновешенные поршни гидравлической машины, пропорциональны площадям (S1, S2) этих поршней.	F1 / F2 = S1 / S2
18. Закон сообщаю-щихся сосудов	Однородная жидкость в сообщающихся сосудах находится на одном уровне (h)	h = const
19. Механическая работа	Работа (A) — величина, равная произведению перемещения тела (S) на силу (F), под действием которой это перемещение произошло.	А = F*S
20. Коэффициент полезного действия механизма (КПД)	Коэффициент полезного действия (КПД) механизма — число, показывающее, какую часть от всей выполненной работы (АВ) составляет полезная работа (АП).	ɳ = АП / АВ *100%
21. Потенциальная энергия	Потенциальная энергия (ЕП) тела, поднятого над Землей, пропорциональна его массе (т) и высоте (h) над Землей.	ЕП = m*g*h
22. Кинетическая энергия	Кинетическая энергия (ЕК) движущегося тела пропорциональна его массе (m) и квадрату скорости (ʋ2).	ЕК = m*ʋ2 / 2
23. Сохранение и превращение механической энергии	Сумма потенциальной (ЕП) и кинетической (ЕК) энергии в любой момент времени остается постоянной.	EП + EК = const
24. Мощность	Мощность (N) — величина, показывающая скорость выполнения работы и равная:а) отношению работы (А) ко времени (t), за которое она выполнена;б) произведению силы (F), под действием которой перемещается тело, на среднюю скорость (ʋ) его перемещения.	N = A / t N = F*ʋ

12 (двенадцать) самых необходимых (самых востребованных) формул по физике в 7 классе:

Независимые события

Два события $А$ и $В$ называются независимыми, если вероятность появления каждого из них не зависит от того,
появилось другое событие или нет. В противном случае события называются зависимыми.

Вероятность произведения двух независимых событий $A$ и $B$ равна произведению этих
вероятностей:

$Р(А·В)=Р(А)·Р(В)$

Иван Иванович купил два различных лотерейных билета. Вероятность того, что выиграет первый
лотерейный билет, равна $0,15$. Вероятность того, что выиграет второй лотерейный билет, равна $0,12$. Иван Иванович
участвует в обоих розыгрышах. Считая, что розыгрыши проводятся независимо друг от друга, найдите вероятность того,
что Иван Иванович выиграет в обоих розыгрышах.

Решения:

Вероятность $Р(А)$ — выиграет первый билет.

Вероятность $Р(В)$ — выиграет второй билет.

События $А$ и $В$ – это независимые события. То есть, чтобы найти вероятность того, что они произойдут оба
события, нужно найти произведение вероятностей

$Р(А·В)=Р(А)·Р(В)$

$Р=0,15·0,12=0,018$

Ответ: $0,018$

Что изменилось в 2022 в ЕГЭ по профильной математике

И начнем мы с инноваций, которые уже официально утверждены ФИПИ. 

1. Изменения, связанные с заданиями:

     Ура, ликуйте, выпускники, ведь количество заданий уменьшилось. Вариант ЕГЭ по профилю будет состоять из 18 заданий. Правда, изменения коснулись самых любимых одиннадцатиклассниками номеров. Так, например, никогда больше в КИМах мы не увидим первого номера. Это звание теперь гордо носит решение простейшего уравнения (в прошлом номер 5). На место привычного 2 задания встал бывший номер 4 — теория вероятности, а на четвертом месте оказалась планиметрия, которая раньше шла шестым заданием.

     Резко позиции сдал номер 9, ставший в обновленной версии базовым 5. Кстати, раньше это задание имело маркировку повышенной сложности. С 8 на 6 перешла стереометрия, а 10 переместилось на 8. Девятой по счету теперь решаем задачу на движение, сплавы и смеси или проценты.

     А вот в “полку” второй части экзамена по профильной математике явно убыло. В геройском бою потеряло свой пункт 5 задание 13 — теперь отбирать нужные корни заданного промежутка не придется.

     Самые крупные изменения в экзамене по профилю потерпел 15 номер. Когда-то давно эксперты решили упростить задание и вместо системы уравнения и неравенства оставили обычные неравенства. Но в этом году все повернулось на 360 градусов (математики, поняли, о чем мы?). Усложненный вариант вновь будет представлять собой систему уравнения и неравенства.

      Вот и все, что касается изменений непосредственно заданий в ЕГЭ по математике профильного уровня 2022. Двигаемся дальше! 

2. Новые задания на профиле 2022: 

     Да-да, новинками в этом сезоне не обделили и ЕГЭ по математике профильного уровня. Что же нас ждет за этой дверью?

     Задание 3 — анализ функций. Формат, который годами игнорировался на экзамене по профильной математике, появился в 2022. Ух, а вот сейчас пристегивайте ремни, мы вплотную приблизились к заданиям повышенной сложности.Номер 10 из блока «Элементы комбинаторики, статистики и теории вероятностей» и задание 11 на комплексные числа, напомним, раньше на ЕГЭ эту тему не затрагивали в принципе (даже у профильщиков). 

3. Критерии оценивания ЕГЭ по профильной математике 

     По традиции экзамен по профильной математике в 2022 году будет оцениваться по давно разработанной системе первичных баллов. Максимальный балл за выполнение работы увеличился за счет сложности 13 задания: подняли с 2 до 3, за номер 15 теперь максимально можно получить 2 балла. В общей сложности за экзамен по профилю теперь можно получить 31 первичный балл.

     “Ну вот получил я, например, 28, а во вторичных-то это сколько?” — обязательно спросите вы. И мы ответим. Для перевода во вторичную систему существует специально разработанная таблица, ориентироваться в которой предельно просто. Ищем количество набранных баллов в первом столбике и смотрим их перевод во втором. Вуаля, вот и ваш результат!

     А сейчас немного про минимальные пороги. Конечно, мы уверены, что вы превзойдете эти баллы в два, три, а то и все 10 раз, но все-таки знать это необходимо. Итак, чтобы получить аттестат и иметь возможность поступить в вуз, нужно набрать 5 первичных=23 вторичных балла. А если ваша мечта — поступление в подведомственные вузы Минобрнауки, то минимумом будет 7 первичных=33 вторичных балла. 

Какие темы важно знать для ЕГЭ по математике 2022?

В математике, как и в любом предмете, есть опорные темы. Если вы их выучите, будет легче справиться с экзаменом.

Формулы тригонометрии

Очень важно знать формулы тригонометрии и уметь применять их. Хорошая новость: в справочных материалах можно найти несколько тригонометрических формул

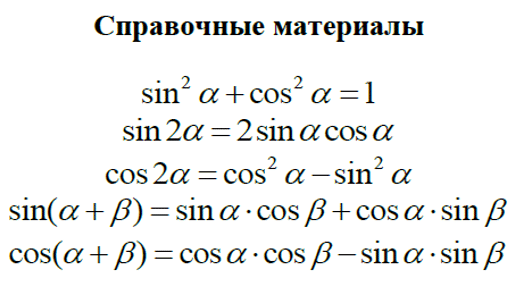
Но формул гораздо больше. Я советую не зубрить их, а научиться выводить: приходить к формулам шаг за шагом, опираясь на тождества. Кстати, мы учим выводить формулы на курсах подготовки к ЕГЭ: это полезно, чтобы оказаться на экзамене во всеоружии и ничего не перепутать.

Квадратные уравнения

Эти уравнения мы учимся решать еще в 7 классе. Они встречаются в ЕГЭ по математике постоянно: и как самостоятельные задания, и внутри более сложных уравнений или неравенств. Квадратные уравнения могут встретиться в математических моделях № 8 и № 15, в задачах на геометрию и стереометрию, в задании № 17 с параметром.

Самое главное — хорошо знать универсальные методы решения. Первый — через формулу дискриминанта, второй — через теорему Виета, которая может сэкономить время на экзамене.

Треугольники

Эта замечательная тема, которую проходят в 7 классе — основа основ всей геометрии. Она нужна и для решения стереометрии. и для простейших планиметрических задач. Еще треугольники необходимы, чтобы освоить огромное количество теорем

Выучите все, что с ними связано! Особое внимание обратите на прямоугольные треугольники, которые встречаются чаще остальных — тогда геометрические задачи сразу станут проще

Проценты

Самая нелюбимая тема моих учеников после тригонометрии, которую необходимо хорошо знать. Проценты нужны для реальной математики — это № 8 (с кратким ответом) и № 15 (с развернутым ответом). Понимание этой темы может принести вам 3 первичных балла.

Геометрия в пространстве (стереометрия)

Главная диагональ куба:

Объем куба:

Объём прямоугольного параллелепипеда:

Главная диагональ прямоугольного параллелепипеда (эту формулу также можно назвать: «трёхмерная Теорема Пифагора»):

Объём призмы:

Площадь боковой поверхности прямой призмы (P – периметр основания, l – боковое ребро, в данном случае равное высоте h):

Объём кругового цилиндра:

Площадь боковой поверхности прямого кругового цилиндра:

Объём пирамиды:

Площадь боковой поверхности правильной пирамиды (P – периметр основания, l – апофема, т.е. высота боковой грани):

Объем кругового конуса:

Площадь боковой поверхности прямого кругового конуса:

Длина образующей прямого кругового конуса:

Объём шара:

Площадь поверхности шара (или, другими словами, площадь сферы):

Теория к заданию 7 из ЕГЭ по математике (профильной)

Производной функции $y = f(x)$ в данной точке $х_0$ называют предел отношения приращения функции к соответствующему приращению его аргумента при условии, что последнее стремится к нулю:

$f'(x_0)={lim}{△x→0}{△f(x_0)}/{△x}$

Дифференцированием называют операцию нахождения производной.

Таблица производных некоторых элементарных функций

Функция	Производная
$c$	$0$
$x$	$1$
$x^n$	$nx^{n-1}$
${1}/{x}$	$-{1}/{x^2}$
$√x$	${1}/{2√x}$
$e^x$	$e^x$
$lnx$	${1}/{x}$
$sinx$	$cosx$
$cosx$	$-sinx$
$tgx$	${1}/{cos^2x}$
$ctgx$	$-{1}/{sin^2x}$

Основные правила дифференцирования

1. Производная суммы (разности) равна сумме (разности) производных

$(f(x) ± g(x))’= f'(x)±g'(x)$

Найти производную функции $f(x)=3x^5-cosx+{1}/{x}$

Производная суммы (разности) равна сумме (разности) производных.

$f'(x) = (3x^5 )’-(cos x)’ + ({1}/{x})’ = 15x^4 + sinx — {1}/{x^2}$

2. Производная произведения

$(f(x) · g(x))’= f'(x) · g(x)+ f(x) · g(x)’$

Найти производную $f(x)=4x·cosx$

$f'(x)=(4x)’·cosx+4x·(cosx)’=4·cosx-4x·sinx$

3. Производная частного

$({f(x)}/{g(x)})’={f'(x)·g(x)-f(x)·g(x)’}/{g^2(x)}$

Найти производную $f(x)={5x^5}/{e^x}$

$f'(x)={(5x^5)’·e^x-5x^5·(e^x)’}/{(e^x)^2}={25x^4·e^x-5x^5·e^x}/{(e^x)^2}$

4. Производная сложной функции равна произведению производной внешней функции на производную внутренней функции

$f(g(x))’=f'(g(x))·g'(x)$

$f(x)= cos(5x)$

$f'(x)=cos'(5x)·(5x)’=-sin(5x)·5= -5sin(5x)$

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Геометрический смысл производной

Напомним, что уравнение прямой, не параллельной осям координат, можно записать в виде $y = kx + b$, где $k$ – угловой коэффициент прямой. Коэффициент $k$ равен тангенсу угла наклона между прямой и положительным направлением оси $Ох$.

$k = tgα$

Производная функции $f(x)$ в точке $х_0$ равна угловому коэффициенту $k$ касательной к графику в данной точке:

$f'(x_0) = k$

Следовательно, можем составить общее равенство:

$f'(x_0) = k = tgα$

На рисунке касательная к функции $f(x)$ возрастает, следовательно, коэффициент $k > 0$. Так как $k > 0$, то $f'(x_0) = tgα > 0$. Угол $α$ между касательной и положительным направлением $Ох$ острый.

На рисунке касательная к функции $f(x)$ убывает, следовательно, коэффициент $k < 0$, следовательно, $f'(x_0) = tgα < 0$. Угол $α$ между касательной и положительным направлением оси $Ох$ тупой.

На рисунке касательная к функции $f(x)$ параллельна оси $Ох$, следовательно, коэффициент $k = 0$, следовательно, $f'(x_0) = tg α = 0$. Точка $x_0$, в которой $f ‘(x_0) = 0$, называется экстремумом.

На рисунке изображён график функции $y=f(x)$ и касательная к этому графику, проведённая в точке с абсциссой $x_0$. Найдите значение производной функции $f(x)$ в точке $x_0$.

Решение:

Касательная к графику возрастает, следовательно, $f'(x_0) = tg α > 0$

Для того, чтобы найти $f'(x_0)$, найдем тангенс угла наклона между касательной и положительным направлением оси $Ох$. Для этого достроим касательную до треугольника $АВС$.

Найдем тангенс угла $ВАС$. (Тангенсом острого угла в прямоугольном треугольнике называется отношение противолежащего катета к прилежащему катету.)

$tg BAC = {BC}/{AC} = {3}/{12}= {1}/{4}=0,25$

$f'(x_0) = tg ВАС = 0,25$

Ответ: $0,25$

Производная так же применяется для нахождения промежутков возрастания и убывания функции:

Если $f'(x) > 0$ на промежутке, то функция $f(x)$ возрастает на этом промежутке.

Если $f'(x) < 0$ на промежутке, то функция $f(x)$ убывает на этом промежутке.

На рисунке изображен график функции $y = f(x)$. Найдите среди точек $х_1,х_2,х_3…х_7$ те точки, в которых производная функции отрицательна.

В ответ запишите количество данных точек.

Решение:

Отрицательным значениям производной соответствуют интервалы, на которых функция $f (x)$ убывает. Поэтому, выделим на рисунке интервалы, на которых функция убывает.

В выделенных интервалах находятся точки $х_2, х_4$. В ответ напишем их количество $2$.

Ответ: $2$

Задача №17, экономическая

Стандартное начало условия:

• 1-го числа каждого месяца долг возрастает на `color(green)(r%)`.
• со 2-го по 14-е число каждого месяца необходимо выплатить часть долга.
• 15-го числа каждого месяца долг должен быть на одну и ту же величину меньше долга на 15-е число предыдущего месяца.

Основная идея решения:

1. каждый месяц (15-го числа) долг должен уменьшаться на одну и ту же величину, т.е. на `1/n` часть изначального долга, т.е. на `color(blue)(S/n)`
2. каждый месяц (1-го числа) банк увеличивает остаток долга на `color(green)(r%)`.
3. каждый месяц (2-14-го числа) клиент выплачивает начисленные проценты (пункт 2) и ежемесячную часть долга (пункт 1).

Составляем таблицу платежей по месяцам:

Взятие кредита:
15 декабря:	Долг = `S` рублей.
1-й месяц:
1 января	Банк начисляет проценты = `color(green)(S*r)`
	Долг = `S + color(green)(S*r)`
2-14 января	Платим `color(green)(S*r) + color(blue)(S/n)`
	Долг = « `– [ color(green)(S*r) + color(blue)(S/n) ] = S-color(blue)(S/n) = (n-1)/n*S`
2-й месяц:
1 февраля	Банк начисляет проценты = `color(green)(obrace((n-1)/n*S)^(«Предыд.долг»)*r)`
	Долг = `(n-1)/n*S+` `color(green)((n-1)/n*S*r)`
2-14 февраля	Платим `color(green)((n-1)/n*S*r)+` `color(blue)(S/n)`
	Долг = `[(n-1)/n*S +` `color(green)((n-1)/n*S*r)]–` `[color(green)((n-1)/n*S*r)+` `color(blue)(S/n)]=` `(n-1)/n*S — color(blue)(S/n)=` `(n-2)/n*S`
3-й месяц:
1 марта	Банк начисляет проценты = `color(green)((n-2)/n*S*r)`
	Долг = `(n-2)/n*S + color(green)((n-2)/n*S*r)`
2-14 марта	Платим `color(green)((n-2)/n*S*r) + color(blue)(S/n)`
	Долг = `[(n-2)/n*S + color(green)((n-2)/n*S*r)] – [color(green)((n-2)/n*S*r) + color(blue)(S/n)] = (n-2)/n*S — color(blue)(S/n) = (n-3)/n*S`
(n-1)-й месяц:	Остаток долга = `2/n*S`
1 мартобря	Банк начисляет проценты = `color(green)(2/n*S*r)`
	Долг = `2/n*S + color(green)(2/n*S*r)`
2-14 мартобря	Платим `color(green)(2/n*S*r) + color(blue)(S/n)`
	Долг = `[2/n*S + color(green)(2/n*S*r)] – [color(green)(2/n*S*r) + color(blue)(S/n)] = 2/n*S — color(blue)(S/n) = 1/n*S`
n-й месяц:	Остаток долга = `1/n*S`
1 апребря	Банк начисляет проценты = `color(green)(1/n*S*r)`
	Долг = `1/n*S + color(green)(1/n*S*r)`
2-14 апребря	Платим `color(green)(1/n*S*r) + color(blue)(S/n)`
	Долг = `[1/n*S + color(green)(1/n*S*r)] – [color(green)(1/n*S*r) + color(blue)(S/n)] = 1/n*S — color(blue)(S/n) = 0`

Геометрия на плоскости (планиметрия)

Пусть имеется произвольный треугольник:

Тогда, сумма углов треугольника:

Площадь треугольника через две стороны и угол между ними:

Площадь треугольника через сторону и высоту опущенную на неё:

Полупериметр треугольника находится по следующей формуле:

Формула Герона для площади треугольника:

Площадь треугольника через радиус описанной окружности:

Формула медианы:

Свойство биссектрисы:

Формулы биссектрисы:

Основное свойство высот треугольника:

Формула высоты:

Еще одно полезное свойство высот треугольника:

Теорема косинусов:

Теорема синусов:

Радиус окружности, вписанной в правильный треугольник:

Радиус окружности, описанной около правильного треугольника:

Площадь правильного треугольника:

Теорема Пифагора для прямоугольного треугольника (c — гипотенуза, a и b — катеты):

Радиус окружности, вписанной в прямоугольный треугольник:

Радиус окружности, описанной вокруг прямоугольного треугольника:

Площадь прямоугольного треугольника (h — высота опущенная на гипотенузу):

Свойства высоты, опущенной на гипотенузу прямоугольного треугольника:

Длина средней линии трапеции:

Площадь трапеции:

Площадь параллелограмма через сторону и высоту опущенную на неё:

Площадь параллелограмма через две стороны и угол между ними:

Площадь квадрата через длину его стороны:

Площадь квадрата через длину его диагонали:

Площадь ромба (первая формула — через две диагонали, вторая — через длину стороны и угол между сторонами):

Площадь прямоугольника через две смежные стороны:

Площадь произвольного выпуклого четырёхугольника через две диагонали и угол между ними:

Связь площади произвольной фигуры, её полупериметра и радиуса вписанной окружности (очевидно, что формула выполняется только для фигур в которые можно вписать окружность, т.е. в том числе для любых треугольников):

Свойство касательных:

Свойство хорды:

Теорема о пропорциональных отрезках хорд:

Теорема о касательной и секущей:

Теорема о двух секущих:

Теорема о центральном и вписанном углах (величина центрального угла в два раза больше величины вписанного угла, если они опираются на общую дугу):

Свойство вписанных углов (все вписанные углы опирающиеся на общую дугу равны между собой):

Свойство центральных углов и хорд:

Свойство центральных углов и секущих:

Условие, при выполнении которого возможно вписать окружность в четырёхугольник:

Условие, при выполнении которого возможно описать окружность вокруг четырёхугольника:

Сумма углов n-угольника:

Центральный угол правильного n-угольника:

Площадь правильного n-угольника:

Длина окружности:

Длина дуги окружности:

Площадь круга:

Площадь сектора:

Площадь кольца:

Площадь кругового сегмента:

Физический смысл производной

Если материальная точка движется прямолинейно и ее координата изменяется в зависимости от времени по закону $x(t)$, то мгновенная скорость данной точки равна производной функции.

$v(t) = x'(t)$

Точка движется по координатной прямой согласно закону $x(t)= 1,5t^2-3t + 7$, где $x(t)$ — координата в момент времени $t$. В какой момент времени скорость точки будет равна $12$?

Решение:

1. Скорость – это производная от $x(t)$, поэтому найдем производную заданной функции

$v(t) = x'(t) = 1,5·2t -3 = 3t -3$

2. Чтобы найти, в какой момент времени $t$ скорость была равна $12$, составим и решим уравнение:

$3t-3 = 12$

$3t = 15$

$t = 5$

Ответ: $5$

Особенности уровней ЕГЭ по математике

В 2015 году ЕГЭ по математике разделили на базовый и профильный уровни. Это упростило жизнь выпускникам, которые не планируют поступать на специальности, связанные с математикой. Если ЕГЭ по математике нужен только для получения аттестата, можно сдать его облегченную версию, оставив время и силы для профильных экзаменов.

Базовый уровень ЕГЭ по математике

Как устроен базовый ЕГЭ по математике? Экзамен идет 180 минут, он состоит из 21 задания, за каждое из которых можно получить 1 балл. Этот экзамен единственный, который переводится не в 100-бальную систему, а в оценки.

Пока перевод баллов ЕГЭ по математике базового уровня в оценки не опубликован ФИПИ, но мы добавим его в статью, как только появится официальная информация.

В ЕГЭ по математике базового уровня 6 тематических блоков:

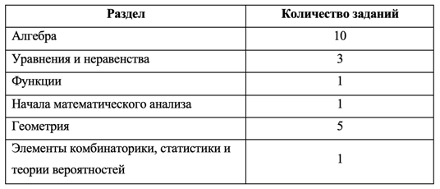
Тематические блоки, ЕГЭ по математике 2022, базовый уровень

Подробнее про базовый ЕГЭ по математике, включая разбор всех заданий, читайте здесь, а мы перейдём к профильному.

Профильный уровень ЕГЭ по математике

Данный экзамен, как и остальные ЕГЭ, переводится в 100-бальную систему.

Пока перевод баллов ЕГЭ по математике профильного уровня в 100-бальную систему пока не опубликован ФИПИ. Мы добавим его в статью, как только появится официальная информация.

Экзамен состоит из двух частей: Часть 1 с кратким ответом, а Часть 2 — с развернутым. Длится он 235 минут. Всего есть 18 заданий, которые разделены на 3 блока: алгебра, геометрия и реальная математика. Максимальное количество первичных баллов — 31.

База, профиль — неважно, к какому именно уровню вы готовитесь. В любом случае надо не только правильно решить каждое задание, но и оформить его так, чтобы проверяющие ни к чему не придрались

Нарисовать и описать график, расписать решение уравнения или задачи… И это не все: нужно еще и внести ответы в бланк без ошибок. И все это — за ограниченный период времени! Так можно перенервничать и запороть даже самую простую задачку. А на ЕГЭ — каждый балл на счету.Поэтому на своих занятиях я сразу показываю своим ученикам, как правильно оформлять каждое задание в ЕГЭ по математике. Мы разбираем все критерии и учимся правильно отвечать на вопросы. А еще я всегда помогаю ученикам закрыть пробелы в знаниях и объясняю сложные темы столько раз, сколько нужно. И куда же без лайфхаков? Всегда рассказываю лучший способ решения типичных заданий. Так что мои ученики приходят на экзамены подготовленными и не нервничают, когда видят задачу. Хотите также? Приходите ко мне на курсы подготовки к ЕГЭ по математике — научу!

Несовместные события

Два события $А$ и $В$ называют несовместными, если отсутствуют исходы, благоприятствующие одновременно как событию
$А$, так и событию $В$. (События, которые не могут произойти одновременно)

Вероятность суммы двух несовместных событий $A$ и $B$ равна сумме вероятностей этих
событий:

$Р(А+В)=Р(А)+Р(В)$

На экзамене по алгебре школьнику достается один вопрос их всех экзаменационных. Вероятность
того, что это вопрос на тему «Квадратные уравнения», равна $0,3$. Вероятность того, что это вопрос на тему
«Иррациональные уравнения», равна $0,18$. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите
вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем.

Решение:

Данные события называются несовместные, так как школьнику достанется вопрос ЛИБО по теме «Квадратные уравнения»,
ЛИБО по теме «Иррациональные уравнения». Одновременно темы не могут попасться. Вероятность суммы двух
несовместных событий $A$ и $B$ равна сумме вероятностей этих событий:

$Р(А+В)=Р(А)+Р(В)$

$Р = 0,3+0,18=0,48$

Ответ: $0,48$

Формулы для ОГЭ-2022 по математике

Формулы сокращённого умножения

`(a + b)^2=a^2 + 2ab + b^2`
`(a − b)^2=a^2 − 2ab + b^2`
`a^2 − b^2=(a + b)(a − b)`
`a^3 + b^3=(a + b)(a^2 − ab + b^2)`
`a^3 − b^3=(a − b)(a^2 + ab + b^2)`
`(a + b)^3=a^3 + 3a^2b + 3ab^2 + b^3`	Эти две формулы заучивать не обязательно, но желательно
`(a − b)^3=a^3 − 3a^2b + 3ab^2 − b^3`

Прогрессии

Геометрическая прогрессия:

`b_n=b_(n-1)*q`

`b_n=b_1*q^(n-1)`

`S_n=((q^n-1)*b_1)/(q-1)`

Бесконечно убывающая: `S=b_1/(1-q)`

Вероятность

Вероятность события A:	`P(A)=m/n`	m — число благоприятных событийn — общее число событий
События происходят A и B происходят одновременно	`A*B`
Независимые события:	`P(A*B)=P(A)*P(B)`	Когда вероятность одного события (А) не зависит от другого события (B)
Зависимые события:	`P(A*B)=P(A)*P(B|A)`	`P(B|A)` — вероятность события B при условии, что событие A наступило
Происходит или событие A, или B	`A+B`
Несовместные события:	`P(A+B)=P(A)+P(B)`	Когда невозможно наступление обоих событий одновременно, т.е. `P(A*B)=0`
Совместные события:	`P(A+B)=P(A)+P(B)-P(A*B)`	Когда оба события могут наступить одновременно

Свойства степеней

`a^0=1`	`a^1=a`
`a^(-1)=1/a`	`a^(-n)=1/a^n`
`a^(1/2)=sqrt(a)`	`a^(1/n)=root(n)(a)`
`a^m*a^n=a^(m+n)`	`a^m/a^n=a^(m-n)`
`(a*b)^n=a^n*b^n`	`(a/b)^n=a^n/b^n`
`(a^m)^n=a^(m*n)`	`a^(m/n)=root(n)(a^m)`

Геометрия

Планиметрия (2D)

Тригонометрия:	`sinA=a/c`   `cosA=b/c`
	`text(tg)A=sinA/cosA=a/b`
Теорема косинусов:	`c^2=a^2+b^2-2ab*cosC`
Теорема синусов:	`a/sinA=b/sinB=c/sinC=2R`	где R — радиус описанной окружности
Уравнение окружности:	`(x-x_0)^2+(y-y_0)^2=R^2`	где `(x_0;y_0)` — координаты центра окружности
Соотношение вписанного и центрального углов:	`beta=alpha/2=(uualpha)/2`
Описанная окружность, треугольник:	`R=(abc)/(4S)`		См. также теорему синусов. Центр лежит на пересечении срединных перпендикуляров.
Вписанная окружность, треугольник:	`r=S/p`		где p — полупериметр многоугольника. Центр лежит на пересечении биссектрис.
Описанная окружность, четырёхугольник:	`alpha+gamma=beta+delta=180^circ`
Вписанная окружность, четырёхугольник:	`a+c=b+d`
Свойство биссектрисы:	`a/x=b/y`
Теорема о пересекающихся хордах:	`AM*BM=CM*DM`		Эти теоремы необходимо уметь выводить
Теорема об угле между касательной и хордой:	`alpha=1/2uuAB`
Теорема о касательной и секущей:	`CM^2=AM*BM`
Теорема об отрезках касательных:	`AB=AC`

Площади фигур:

Физика 8: все формулы и определения

«Физика 8: все формулы и определения» — это Справочник по физике в 8 классе, доступный для скачивания в 2-х форматах: КРУПНО (формат PDF, на 4-х страницах) и МЕЛКО (формат JPG, на 1-й странице).

1 файл(ы) 4.29 MB

Физика 8 класс. Все формулы и определения МЕЛКО на одной странице

1 файл(ы) 3.66 MB

В пособии «Физика 8: все формулы и определения» представлено 23 формулы
и определения за весь курс Физики 8 класса:

Глава 1. Тепловые явления

• § 1. Тепловое движение. температура
• § 2. Внутренняя энергия
• § 3. Способы изменения внутренней энергии тела
• § 4. Теплопроводность
• § 5. Конвекция
• § 6. Излучение
• § 7. Количество теплоты. Единицы количества теплоты
• § 8. Удельная теплоёмкость
• § 9. Расчёт количества теплоты, необходимого для нагревания тела или выделяемого им при охлаждении
• § 10. Энергия топлива. Удельная теплота сгорания
• § 11. Закон сохранения и превращения энергии в механических и тепловых процессах
• § 12. Агрегатные состояния вещества
• § 13. Плавление и отвердевание кристаллических тел
• § 14. График плавления и отвердевания кристаллических тел
• § 15. Удельная теплота плавления
• § 16. Испарение. Насыщенный и ненасыщенный пар
• § 17. Поглощение энергии при испарении жидкости и выделение её при конденсации пара
• § 18. Кипение
• § 19. Влажность воздуха. Способы определения влажности воздуха
• § 20. Удельная теплота парообразования и конденсации
• § 21. Работа газа и пара при расширении
• § 22. Двигатель внутреннего сгорания
• § 23. Паровая турбина
• § 24. КПД теплового двигателя

Глава 2. Электрические явления

• § 25. Электризация тел при соприкосновении. Взаимодействие заряженных тел
• § 26. Электроскоп
• § 27. Электрическое поле
• § 28. Делимость электрического заряда. Электрон
• § 29. Строение атомов
• § 30. Объяснение электрических явлении
• § 31. Проводники, полупроводники и непроводники электричества
• § 32. Электрический ток. Источники электрического тока
• § 33. Электрическая цепь и её составные части
• § 34. Электрический ток в металлах
• § 35. Действия электрического тока
• § 36. Направление электрического тока
• § 37. Сила тока. Единицы силы тока
• § 38. Амперметр. Измерение силы тока
• § 39. Электрическое напряжение
• § 40. Единицы напряжения
• § 41. Вольтметр. Измерение напряжения
• § 42. Зависимость силы тока от напряжения
• § 43. Электрическое сопротивление проводников. Единицы сопротивления
• § 44. Закон Ома для участка цепи
• § 45. Расчёт сопротивления проводника. Удельное сопротивление
• § 46. Примеры на расчет сопротивления проводника, силы тока и напряжения
• § 47. Реостаты
• § 48. Последовательное соединение проводников
• § 49. Параллельное соединение проводников
• § 50. Работа электрического тока
• § 51. Мощность электрического тока
• § 52. Единицы работы электрического тока, применяемые на практике
• § 53. Нагревание проводников электрическим током. Закон Джоуля—Ленца
• § 54. Конденсатор
• § 55. Лампа накаливания. Электрические нагревательные приборы
• § 56. Короткое замыкание. Предохранители

Глава 3. Электромагнитные явления

• § 57. Магнитное поле
• § 58. Магнитное поле прямого тока. Магнитные линии
• § 59. Магнитное поле катушки с током. Электромагниты и их применение
• § 60. Постоянные магниты. Магнитное поле постоянных магнитов
• § 61. Магнитное поле земли
• § 62. Действие магнитного поля на проводник с током. Электрический двигатель

Глава 4. Световые явления

• § 63. Источники света. Распространение света
• § 64. Видимое движение светил
• § 65. Отражение света. Закон отражения света
• § 66. Плоское зеркало
• § 67. Преломление света. Закон преломления света
• § 68. Линзы. Оптическая сила линзы
• § 69. Изображения, даваемые линзой
• § 70. Глаз и зрение

Физика 8: все формулы. Таблица 1

Физика 8: все формулы. Таблица 2

Что в итоге

Теперь вы знаете больше про ЕГЭ по математике 2022

Вы познакомились со структурой и поняли, на что стоит обращать внимание при подготовке. А еще узнали, что первую часть обязательно решать на максимум, а вторая не такая страшная, как кажется

Но наверняка у вас еще осталась куча вопросов: по оформлению и конкретному решению каких-то заданий точно.Обо всем этом я подробно рассказываю своим ученикам во время подготовки к ЕГЭ по математике. Мы изучаем все непонятные темы, а потом прорешиваем много однотипных заданий — так легче запоминается формат. Еще мы всегда проводим пробные экзамены, чтобы выявить слабые места. Я анализирую ошибки каждого ученика и индивидуально разбираю их с ними. Благодаря этому мои выпускники гарантированно сдают ЕГЭ на 80+. Если вы хотите оказаться среди них — записывайтесь на курсы!